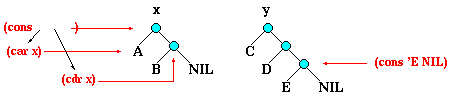
Consider the binary trees x and y below.

In Lisp, x is written as the list '(A B) or, equivalently, as
'(A B . NIL). Similarly, y may be written '(C D E).
Suppose we wish to replace the right-most tip of x
by the entire tree y. This is denoted (app x y), where app
stands for ``append''.
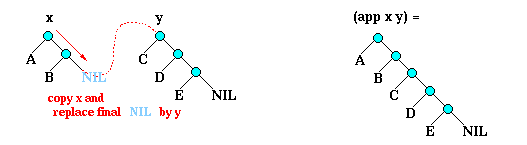
We can define app with:
(defun app (x y) ; Concatenate x and y.
(declare (type (satisfies true-listp) x)); We expect x to end in NIL.
(cond ((endp x) y) ; If x is empty, return y.
(t (cons (car x) ; Else, copy first node
(app (cdr x) y))))) ; and recur into next.
If you defined this function in some Common Lisp, then to run
app on the x and y above you could then type
(app '(A B) '(C D E))and Common Lisp will print the result
(A B C D E).