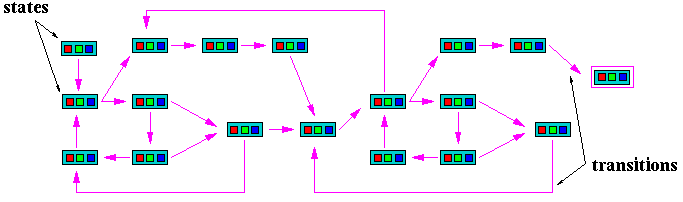

Computing machines, whether hardware or software or some combintation, are frequently modeled as ``state machines.''
To so model a computing machine we must represent its states as objects in our mathematical framework.
Transitions are functions or relations on state objects.
In what language shall we define these objects, functions, and relations?
The mathematical languages we were taught in high school
algebra,
geometry,
trignometry, and
calculus
are inappropriate for modeling digital systems. They primarily let us talk about numbers and continuous functions.
To see what kind of expressive power we need, take a closer look at what a typical state contains.